Log Pearson Type III
Distribusi Pearson III dan Log-Pearson III, sering digunakan pada perhitungan hujan harian maksimum untuk menghitung besarnya banjir rencana yang terjadi pada periode ulang tertentu. Kedua metode ini memiliki konsep yang serupa, namun pada metode Log-Pearson III, persamaan umum analisis frekuensinya terlebih dahulu dilogaritmakan. Namun, besaran faktor frekuensi yang digunakan memiliki besaran yang sama. Kedua besaran faktor frekuensi tersebut dapat diestimasikan dengan persamaan berikut ini (Kite, 1977):
Keterangan:
Distribusi Log Pearson Ill merupakan clistribusi yang fleksibel untuk analisa frekuensi atas data hidrologi. Parameter statistik yang diperlukan ada 3, yaitu:
- Harga rata-rata (mean)
- Penyimpangan baku (standard deviation)
- Koefisien kemencengan (skewness)
Ada 12 distribusi Pearson, tapi hanya distribusi Log Parson III yang dipakai dalam analisa frekuensi atas data hidrologi. Tidak ada syarat khusus untuk distribusi ini, disebut Log Pearson III karena menggunakan 3 parameter statistic dalam proses analisanya. Prosedur perhitungannya adalah:
- Mengubah data debit/hujan sebanyak n buah ($X_1$, $X_2,$ ... $X_n$) menjadi $Log X_1$, $Log X_2$, ....... $Log X_n$
- Menghitung harga rata-rata: $$\overline {Log X} = \frac{\sum_{i=1}^{n} Log X_i}{n}$$
Keterangan:
$\overline {Log X}$:Rata-rata dari Log data$Log X_i$:Logaritma data ke-i$n$:Jumlah data - Menghitung harga simpangan baku (dalam log): $$S = \sqrt{\frac {\sum_{i=1}^{n} (Log X_i - Log X)^2} {n-1} }$$
Keterangan:
$S$:Simpangan baku$n$:Jumlah data$Log X_i$:Nilai logaritma dari data ke-i$\overline{Log X}$:Rata-rata logaritma dari seluruh data - Menghitung koefisien kepencengan (dalam log): $$C_s = \frac {n\sum (Log X - \overline{Log X})^3} {(n-1)(n-2)S^3}$$
Keterangan:
$C_s$:Koefisien skewness$n$:Jumlah data$X$:Data$\overline{X}$:Rata-rata data$S$:Simpangan baku (standar deviasi) - Menghitung nilai ekstrem: $$Log X = \overline {Log X} + G \cdot S$$
Keterangan:
$G$:Nilai koefisien distribusi Log-Pearson III (lihat tabel), fungsi dari koefisien skewness$C_s$:Koefisien skewness - Mencari antiLog dari LogX untuk rnendapatkan hujan (debit banjir) rancangan yang dikehendaki.
Nilai koefisien distribusi kedua metode ini ditentukan tidak hanya dari derajat kepercayaan dan periode ulang rencana, tetapi juga koefisien kecondongan dari seri data yang ada, seperti dapat dilihat pada tabel di bawah ini.
Tabel. Nilai koefisien distribusi Pearson III dan Log-Pearson III
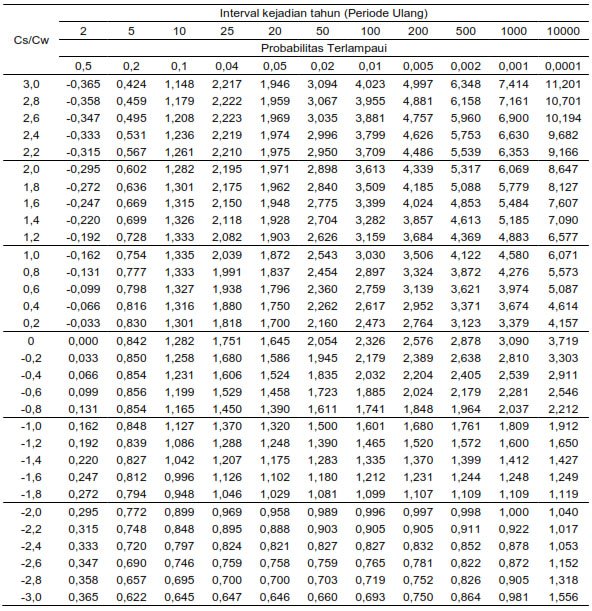
Referensi: Modul 1 Analisa Curah Hujan, Balai Teknik Bendungan
Tags: curah hujan debit

