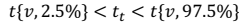Sebelum melakukan analisis data hujan, baik dari pos pengamatan hujan atau data satelit, penting untuk melakukanan pemeriksaan data hujan melalui beberapa uji penting. Uji data hujan ini mencakup uji pencilan (outlier test), uji kecenderungan (trend test), uji kestabilan terhadap rata-rata dan simpangan baku (stability test to mean and variance), dan uji kemandirian (independence test). Sebagai langkah pertama, ada persyaratan yang harus dipenuhi, yaitu menghapus data hujan yang memiliki nilai di bawah 50 mm.
Untuk proses penyusunan hujan rencana, yang perlu diperiksa adalah seri data hujan harian maksimum tahunan (HHMT). Berikut adalah penjelasan rinci tentang proses dari masing-masing uji tersebut.
1. Uji Outlier
Outlier, atau pencilan, adalah nilai yang sangat berbeda dari data lainnya, baik terlalu besar maupun terlalu kecil. Meskipun hujan adalah kejadian yang bersifat stokastik, nilai hujan dapat dianalisis secara statistik dengan pendekatan tertentu. Kesalahan pencatatan data hujan, baik karena kesalahan manusia atau alat pencatat hujan, dapat mempengaruhi analisis dan menghasilkan data yang tidak akurat.
Untuk memeriksa keberadaan outlier atas atau outlier bawah, digunakan metode yang dikembangkan oleh Water Resource Council (1981). Proses pemeriksaan outlier dilakukan berdasarkan koefisien skewness dari data sampel, sebagai berikut:
- Jika koefisien skewness > +0,4, maka perlu dilakukan pemeriksaan untuk outlier atas.
- Jika koefisien skewness < -0,4, maka perlu dilakukan pemeriksaan untuk outlier bawah.
- Jika koefisien skewness berada di antara -0,4 dan +0,4, maka perlu dilakukan pemeriksaan untuk outlier atas dan bawah sebelum memutuskan data mana yang harus dihapus.
Apabila ditemukan outlier atas, perlu dilakukan verifikasi lebih lanjut untuk memastikan kebenaran data tersebut. Jika ditemukan outlier bawah, data tersebut dapat langsung dihapus. Jika data outlier atas tidak dapat dibuktikan kebenarannya secara ilmiah, maka data tersebut harus dibuang terlebih dahulu sebelum digunakan dalam analisis hidrologi lebih lanjut.
Persamaan frekuensi untuk mendeteksi adanya outlier adalah:

Keterangan:
YH,L : Batas (threshold) dari outlier atas dan bawah, dalam logaritma
y : Nilai rata-rata dari data dalam bentuk logaritma
Kn : Konstanta uji outlier, merupakan fungsi dari jumlah data sampel
Sy : Simpangan baku dari data dalam bentuk logaritma
Nilai dari konstanta uji outlier dapat dilihat pada tabel di bawah.

2. Uji Trend
Sebelum digunakan untuk analisis, suatu seri data hidrologi harus dipastikan terlebih dahulu bebas dari adanya trend (kecenderungan), yaitu korelasi antara urutan data dengan peningkatan (atau penurunan) besarnya nilai data tersebut. Secara umum, uji trend dilakukan untuk periode seluruh data yang ada, walaupun dapat juga dilakukan hanya pada periode data yang dicurigai terdapat trend.
Untuk mengetahui adanya trend, digunakan metode Spearman’s rank-correlation. Metode ini didasarkan pada Spearman rank-correlation coefficient, Rsp, yang didefinisikan sebagai:
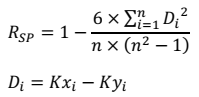
Keterangan:
n : Jumlah sampel
Di : perbedaan antara rank variabel xi, Kxi, (data diurutkan dari kecil ke besar) dan rank berdasarkan nomor urut data asli, Kyi
Bila ada ties, yaitu ada dua atau lebih data dengan nilai sama, maka rank Kxi diambil sebagai nilai rata-rata. Uji eksistensi trend dilakukan dengan menggunakan formulasi berikut:
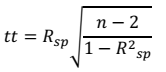
Dimana tt mempunyai distribusi Student’s t dengan derajat kebebasan = n – 2. Distribusi Student’s t dengan significance level 5% dapat dilihat pada lampiran. Seri data yang diuji tidak mengandung trend bila memenuhi:
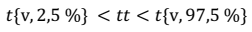
3. Uji Stabilitas
Dalam uji kestabilan ini dilakukan untuk mengetahui data stasioner atau tidak. Secara umum terdapat dua uji yang dilakukan varian dan mean berupa uji F dan T, dimana uji F distribusi dari rasio variannya mengikuti distribusi normal dan mengindikasikan stabilitas dari varian. Uji F digambarkan dengan persamaan:
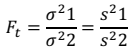
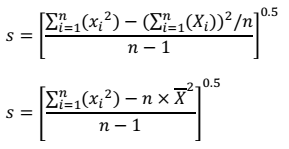
Keterangan :
Ft : stabilitas yang indikasinya dapat diterima, s : deviasi standar skala sampel, Xi : data pengamatan dan n : jumlah total data sampel.
Data menunjukkan kestabilan varian dengan tingkat kesalahan 5% apabila Ft < F{v1,v2,97.5%}
Pemeriksaan stabilitas mean dilakukan dengan menggunakan uji T (distribusi Student’s t). Dalam uji ini, seperti halnya uji stabilitas variance, maka data dibagi dua atau tiga sama besar, kemudian dihitung nilai rata-rata (mean) dari masing-masing sub-sampel tersebut dan dibandingkan. Kesamaan nilai mean ini diuji secara statistik sebagai berikut:
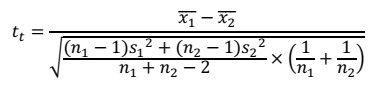
Nilai mean dari sampel dikatakan stabil apabila :